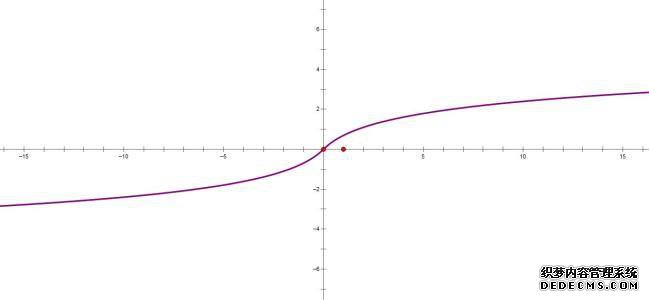
测试点名称:函数的单调性与导数的导数和函数的单调性之间的关系:
(1)如果f'(x)0在(a,b)中始终为true,则f(x)是(a,b)的增长函数和f'(x)0的解集的交集域的相应间隔是增加间隔。(2)如果f'(x)0在(a,b)处恒定,则f(x)是(a,b)的递减函数。f'(x)0解集交点的相应区间定义域是减法区间。
使用导数求解多项式函数的单调性的一般步骤:
1确定f(x)的面积。计算二阶导数f'(x)。3找到f'(x)= 0的根。4使用路线f'(x)= 0定义f(x)的定义。该域分为几个间隔。该列表以这些间隔查看f'(x)的符号,然后确定f(x)的单调间隔。对于f'(x)0,f(x)是相应的间隔增加函数。相应的间隔正在增加。对于f'(x)0,f(x)是相应的间隔减小函数,而相应的间隔是负间隔。
特别是,它让人联想到函数的导数和函数的单调性:
如果在给定间隔中有有限数量的点,并且f'(x)= 0和f'(x)0在其余点上恒定,则f(x)仍然是一个递增函数(即,间隔f'(x)0 in是使f(x)在该间隔内成为增长函数的充分条件,而不是必要条件。
以上内容是Magic Square的学习社区(www。
Mofunge
Com)未经许可不得播放原始内容!